|
A
PROOF OF THE PYTHAGEREAN THEOREM …. For Dummies By Rene M. Rogers |
||||
|
The year was 1953. The
Cold War was in full swing and serious people were building well stocked
underground bomb shelters in their back yards if they could afford to do
so. Little kids in school were doing bomb drills in their
classrooms, much as we did fire drills when I was in public school.
The alarm would go off and the kids would crawl under their desks
and close their eyes with their heads down under their hands.
The possibility of a nuclear bomb exchange between the USA and
Russia was considered a real possibility.
The Rosenbergs had recently (May 1953) been executed for revealing
Atom Bomb secrets to Uncle Joe Stalin in Russia.
Whittiker Chambers had blown the whistle on Alger Hiss, a high
State Department official, as a Russian Spy.
Joe McCarthy, a US Senator, was frothing at the mouth about
Communists in our government and in Hollywood and under almost every bed.
My mother-in-law saw Joe McCarthy as a heaven sent savior while I
saw her and Popo as heaven sent so far as Kay and I and the baby were
concerned. From what I could
see, however, I didn't care too much for McCarthy, but I didn't say
anything. Several of us at Bell Labs began discussing these matters at lunch and coffee breaks and the question arose as to what were the most fundamental building blocks of our technology that we would need to rediscover if our world was destroyed and we had to reconstruct it all from first principles. Most of us were keenly aware that the basic tools we used everyday were mostly taken for granted without much thought as to how those tools were constructed in the first place. This was a matter I had brought up with my mentor, Jay, when I was about 14 years old. Jay, an auto mechanic, found the subject very distasteful. Wrenches and screw drivers were A GIVEN in his mind and asking questions about how they came to be was something he didn't understand at all. As an arrowhead collector, I suggested to the others the making of stone tools as a fundamental technology we ought to know more about, but I had no better luck with flint knapping this time than I'd had before, so that matter was dropped. There were a number of basic ideas under consideration, but it was finally decided that we would concentrate on learning how to make fire without matches and how to derive the Pythagorean Theorem from scratch, the way the master himself did it. A small group of people from the mathematics department and one or two of their bridge partners who were Patent Attorneys agreed to serve as final arbiters of our work with regard to the Pythagoras Theorem.
I had 3 textbooks where the P.T. was introduced, but none of them
went to any effort to derive it from first principles.
It was simply stated as a fact, although one textbook had a figure
showing a right triangle with squares drawn off the 3 sides along with the
statement that the area of the large square off the hypotenuse was exactly
equal to the sum of the areas of the two smaller squares.
Willis Yocom and I collaborated on the following
"derivation" which was summarily rejected by the arbiters,
although it still has the ring of truth so far as I am concerned
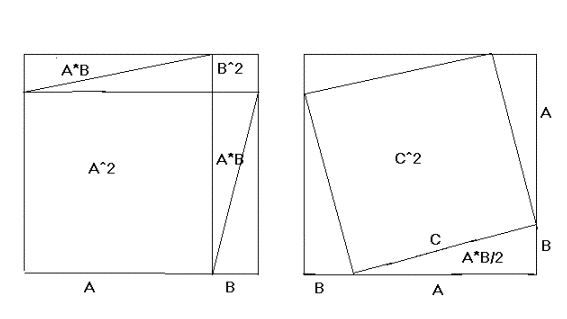
The 2 large squares, A+B on a side, are
identical. The
total area of the figure on the left is (A+B)^2 = A^2
+ B^2 + 2AB . The total area of the figure on the
right is C^2
plus the 4 triangles. These
4 triangles are identical to the 4 triangles in the figure
on the left and the total area of the 4 triangles is just
2AB. It should
be clear to most simple people that C^2 = A^2 +
B^2. This result has been known as the
Theorem of Pythagoras since Ancient Greek times.
The
duplicate bridge crowd rejected our proof on several grounds.
The argument that, if X + Y + Z
= W + Z, then it
follows that X + Y = W, while perfectly true and acceptable, was not
available to Pythagoras. This
innovation is one of the postulates of Algebra, and Pythagoras had no
knowledge of Algebra which didn't come along for yet another 700 years or
so. Algebra, by some
accounts, was due to an Arab olive oil merchant, one
Al Jebra, who invented
and gave his name to a process for manipulating numbers by the use of
symbols. He is said to have
found a practical use for the resulting arguments to keep tabs on his
substantial 'accounts receivable'. I
think the purists also had a problem with our assumption that the 4
triangles in the figure on the right had the same area as the 2 rectangles
in the figure on the left. All
of the other derivations offered were also rejected, but I have no
recollection of any of the details.
The fire making project was taken over by several technicians
working under the spiritual guidance of George Helmke.
Several of these people had children in the Boy Scouts where making
fire using a bow to spin a stick against a tapered hole in a wooden board
was a routine exercise, but
there was convincing evidence that some people could turn the stick
between their hands and make fire... a much more difficult operation. There were also those who argued that this effort was
degenerate since the ancients had little or no need to make fire using
friction. Nature provided
them with plenty of fire from lightening strikes and volcanic activity.
All the people had to do was to learn to keep a few large scraps of
wood burning along with an adequate supply of dry wood. Of course, once someone screwed up and let the fire get wet
or otherwise go out it might be a while before lightening or volcanic
activity gave them a new start. Rubbing
two pieces of wood together to form a hot coal could be powerfully useful
in this case.
There was a somewhat humorous end to the fire making project.
No one ever actually made a fire, but the biggest and strongest
technician on hand, one Albert, came pretty close.
He had resorted to the bow method of spinning the stick and he was
on his knees on the floor in a room used by everyone for general dirty
work, laboring mightily. There was a lathe and a milling machine and a drill press in
this room along with an area where soldering, brazing, and light welding
could be done with a torch. A
half dozen or so technicians were on hand taking in the show as Albert was
producing a great quantity of smoke.
When a large red coal could be seen glowing in the hole, Albert
stopped bowing and began preparing to put some fine tinder in the hole and
to start blowing the coal in the traditional way.
But just as he was preparing this operation, a large drop of sweat
fell off the end of his nose right on the coal, putting it out... a
message from The Gods, perhaps. Albert
and everyone else left in disgust. That
was the end of the fire making exercise, with one exception.
That evening, after almost everyone had left for the day, Willis
and I were on our way out when we passed the dirty work room to find
another technician trying his luck using the drill press, instead of the
bow, to spin the stick. He
was making a lot of smoke, but when he saw us he gave out a silly laugh
and turned away and followed the two of us out of the building.
After the project of finding a proof of the Pythagorean Theorem
was history, one of the senior people in the department (probably
Al Clogston) suggested to me that perhaps Pythagoras had never bothered to
offer a proof. The result was
satisfying to his intuition and it worked out to be true in every case
that anyone bothered to look into further, so that was that.
He went on to tell me that there were a number of useful theorems
in mathematics that no one had ever come up with a rigorous proof
sufficient to satisfy the duplicate bridge class of folks.
Fermat's Last Theorem was a case in point.
Every math student who had gone past high school Algebra knew about
the 3, 4, 5 right triangle (and an infinite set of other triangles with
like properties) in which the hypotenuse was 5 units long while the other
sides were 3 and 4 units long. By
the Pythagoras Theorem
3^2 + 4^2 = 5^2 or
9 + 16 = 25 Fermat
was a recognized math wonder and he apparently left a note in the margin
of one of his papers that he had discovered a wonderful proof of the
proposition that there could be no exact solutions to equations of this
form for integer exponents greater than 2. Unfortunately, Fermat had run
out of paper and did not spell out his proof.
Perhaps the greatest question among pure mathematicians of the day
was, "Is Fermat's Last Theorem true?"
A proof was finally articulated in the 1990's or thereabouts.
A similar situation surrounded Gauss' famous "Central Limit
Theorem" in statistics... the basis of the ubiquitous Bell Shaped
Curve everyone who has ever studied statistics is more than familiar with.
Gauss, according to my informant, agonized for years trying to find
a proof, all the while knowing the truth of his discovery.
It was left to Norbert Weiner who worked in a think tank devoted
mainly to code breaking during WWII to finally come up with a formal proof
satisfying to all. John
Pierce, according to my informant, was a master at offering mathematical
expressions to describe the performance of complex microwave networks.
These expressions were often shown to be not exact in a
mathematical sense, but quite close when compared to experimental results.
No one, including Pierce himself, seemed to know how he did it.
|
||||